2020년 02월 11일 02:12무선 네트워크/Channel State Information

Precise Power Delay Profiling with Commodity Wi-Fi

본문

CSI에서 제시하는 각 성분에 대해 더 자세히 이해하기 위해 읽게 된 논문이다. ACM MobiCom과 IEEE TMC에 등재되었는데, 더 많은 리뷰를 거친 듯한 TMC의 것을 읽었다.

IEEE Explore (2018) / ACM Library (2015)

Introduction

이 논문에서는 더 정확한 Power Delay Profile (PDP) 분석 및 활용을 위해 인접한 채널의 CSI를 이어 큰 Bandwidth에 대한 CSI 정보를 얻고자 했다.

Power Delay Profile의 시간축 Resolution은 신호의 대역폭에 따라 결정되는데 ^[각주:1]^[각주:2], 20MHz로 샘플링을 할 경우 감지할 수 있는 Multipath의 거리 차이는 최소 약 15m ($c \times (\frac{1}{20e+6})=14.9896$)이다. 만일 대역폭을 늘려 80MHz가 된다면, 감지할 수 있는 거리 차이는 최소 약 4m ($c \times (\frac{1}{80e+6})=3.7474$)로 줄어든다. 더욱 정확한 프로파일 분석이 가능해지는 것이다.

하지만 인접한 채널의 CSI를 그대로 이어붙이는 건 불가능했다. 회로의 부정확함과 통신에 영향을 주지 않는 결함이 컸기 때문이다. 따라서, 이 논문에서는 그러한 여러 오류를 어떻게 보상할 수 있을지에 대해 연구하였고, 시변 채널에 대해 얼마의 주기로 보상 값 계산을 해야하는지 등의 시스템 설계를 진행하였다.

Phase 값 이어 붙이기

이어붙이기 전에 몇 가지 문제를 해결해야 한다.

값의 겉보기 형태적 문제 (Non-linear Error)

자연의 신호는 연속이고, Phase는 선형이지만 실제 신호를 합쳐보거나 신호를 보면 그렇지 아니했다.

그래프에서 Phase값이 직선이 아니다.

원래 Propagation 거리 ($d$)가 일정하다면 주파수에 따른 Phase 값($\phi_k$)은 일정히 증가해야 한다.

$$\phi_k=2\pi( f_0+k\Delta f)\frac{d}{c}$$

하지만 Tx-Rx를 안테나를 써봐도, 안테나 대신 유선으로 땡깡 이어보아도 그러지 못했다. 즉, 아래의 (a), (b), (c)에서 직선 형태가 관찰되지 않았다.

(좌) 유선으로 Tx/Rx 칩을 이어 본 결과. 다른 색깔은 다른 칩이다. (우) 예상되는 결과.

서브캐리어 중간 부분은 어느 정도 직선 형태를 띄었는데, 양쪽 가에서는 그러지 못했다. 다만 이 Phase 왜곡 값은 모든 채널에서 각 서브캐리어에 대해 동일하게 나타났으므로, 칩마다 그 상수값을 측정하여 보상하면 된다.

개인적으로 이 내용을 구현해볼 때는 다음과 같이 했다.

40 MHz 채널에 대해서는 이 보정을 적용하기 이전에 아래의 Phase 튀는 문제의 보정을 먼저 적용했다.

% original_phase = o_phase
% linearified phase = l_phase
phase_newavg = mean(l_phase);
if size(o_phase, 2) == 114
  phase_center = mean(phase_newavg(39:76));
  phase_grad = mean(gradient(phase_newavg(39:76)));
else
  phase_center = mean(phase_newavg(19:36));
  phase_grad = mean(gradient(phase_newavg(19:36)));
end

syms x;
phase_line = x * phase_grad + phase_center;

if size(o_phase, 2) == 114
  phase_lindiff = phase_newavg - double(subs(phase_line, [-58:-2 2:58]));
else
  phase_lindiff = phase_newavg - double(subs(phase_line, [-28:-1 1:28]));
end

for i = 1:size(o_phase, 1)
  l_phase(i, :) = l_phase(i, :) - phase_lindiff;
end

이렇게 구현하면 아래와 같은 결과가 나온다.

40MHz 채널 중간에서 Phase가 튄다.

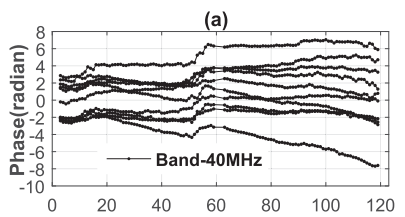
튄다. 위 그래프에서 아래 50-60 사이를 보면 훅 올라가는 구간이 있다. 이는 이 사람들이 조사해 본 결과 항상 일정한 값 (이 사람들 기기에서는 약 1.7rad)을 유지하는 경향이 있는 것이 확인되어 그냥 상수로 조사하여 보상해주면 된다.

개인적으로 이 내용을 구현해볼 때는 다음과 같이 했다.

% original phase = o_phase
% linearified phase = l_phase
if size(o_phase, 2) == 114
  phase_avg = mean(o_phase);
  phase_diff = phase_avg(58) - phase_avg(57) + ( ...
      (phase_avg(56) - phase_avg(41) ...
      + phase_avg(74) - phase_avg(59)) / 30 ...
      ) * 4;
  for i = 1:size(o_phase, 1)
      l_phase(i, :) = [ ...
          o_phase(i, 1:57) (o_phase(i, 58:114)' - phase_diff) ...
      ];
  end
end

이렇게 구현하면 아래와 같은 결과가 나온다.

위 두가지를 동작 인식에 사용할 수 있을까?

물론 사용할 수 있다. 하지만 결국 이상적으로 생각해보면 CSI의 Phase 데이터로부터 얻는 것은 하나의 일차방정식일 것이기 때문에, 위의 Nonlinear Error를 보상하는 것보다는 아래의 Linear Error를 보상하는 것이 훨씬 그 정확도를 높일 것이다. 컴퓨팅 리소스도 아낄 겸...! 뉴럴넷이 해결해줄거야...!

선형성에는 영향이 없는 오류들 (Linear Error)

이제부터는 겁나 어렵다.

안테나로부터 CSI를 얻는 과정은 위와 같은데, Phase값에 오류가 생기는 부분과 그 오류는 (그림에는 나와있지 않지만) Up/Downconverter에서 CFO, Packet Detector에서 Packet Detection Uncertainty (시간 오류), DAC/ADC에서 SFO이다.이다. CFO는 그림에 나와있듯이 CFO Corrector에서 어느정도 보상이 가능하다. 하지만 여전히 CFO 문제는 조금 남아있게 된다. AGC가 일으키는 문제는 추후 Amplitude 값 오류 해결 부분에서 다룬다.

Packet Boundary Detection Uncertainty 제거

들어오는 신호와 칩의 샘플링 주기가 정확하게 맞아 떨어지지 않는 이상, Packet Boundary Detection Error는 작은 범위 내에서 항상 일어나기 마련이다. 802.11n 칩은 Packet Boundary를 20MHz로 체크하므로, 아마 많아야 0.00000005초 이내로 차이가 날 것이라고 나는 생각하고 있다. 아무튼 PBD 에러는 거의 무조건 발생하는데, 이로 인해 실제 패킷의 시작 부분과 차이가 나는 만큼 Time Delay($\tau_b$)가 생긴다.

이 논문에서 인용한 [20]번째 문서^[각주:3]에 따르면 이 PBD 오류는 오류가 없는 점($\tau_b=0$)을 기준으로 가우시안 분포를 이룬다고 한다. 그리고 이 논문에서는 그를 직접 증명하는데, 실제로 가우시안 분포이다.

가우시안 분포를 따르는 오류는 어떻게 해결하는가?! 평균내면 된다. 그럼 영에 수렴할 터이다.

측정하려는 임의의 밴드 $b$에서 평균을 계산하기 위해 모을 패킷의 개수를 $n_b$라 하면...

$$\bar{\phi}^b_k=\sum^{n_b}_{i=1}\phi^b_k(i)/n_b$$

이다. 여기서 $i$는 측정한 Packet의 번호이고, $k$는 서브캐리어의 번호이다. 즉, 각 밴드 각 서브캐리어마다 몇개의 CSI를 모아 평균을 때린다는 것이다.

이 보정을 동작 인식에 사용한다고 생각해보자. 분명... Phase 변화가 더 부드러워질 것이다. 하지만 우리의 뉴럴넷은 어느정도의 노이즈는 받아주므로 뉴럴넷에 넣을 데이터에 이 전처리는 안 해줘도 될 것이다.

Sampling Frequency Offset 제거

SFO는 DAC와 ADC 사이의 샘플링 Frequency 차이인데, Tx와 Rx의 샘플링 주파수를 각각 $f_t$, $f_r$이라고 하면 이들로 인해 일어날 수 있는 Offset의 최소 배수 (fractional difference)를 $\zeta=\frac{f_t}{f_r}-1$이라고 할 수 있다. SFO를 $\phi_k$에서 제거하려면 $\phi_k$에다 $e^{-j\cdot \zeta'\cdot k}$를 곱하면 될 것이다. $j$는 허수, $\zeta'$는 fractional difference의 배수이다.

그렇다면 저 SFO($\zeta'$, 아래에서는 $\epsilon$)는 어떻게 구하는가? 이 논문의 저자들은 같은 환경 및 조건에서 여러 밴드에 대해 CSI를 측정할 경우 같은 Multi Path를 거치기 때문에, PBD로 인한 오류를 제거한 다음의 Phase값이 만일 SFO가 없다면 밴드 관계 없이 모두 동일해야 한다는 점을 이용했다. ^[각주:4]

for each Wi-Fi Band Pair "$c$" do  
    Record the top-two local maximal similarity values and the  
    corresponding $\epsilon:<\epsilon^c_1,\rho^c_1>$ and $<\epsilon^c_2,\rho^c_2>$.  
Clustering on $\epsilon$ and find the cluster with the maximal similarity sum.  
Return the cluster center as the final $\epsilon$ value.

알고리즘을 해석해보자면, 두 밴드의 페어를 $c$라 하고, 한쪽 밴드에 $\epsilon^c$만큼을 곱하여 "rotate" 시킨 뒤, 두 밴드의 Phase 유사도를 $\rho^c$라 하며, 그들을 저장하여 클러스터링하여 가장 유사도가 높은 곳의 $\epsilon$값을 SFO로 추정하겠다는 것이다.

이런 결과가 나오며, 여기서는 $\epsilon=0.75$ 정도가 가장 유사도($\rho$)가 크게 나왔다.

컴퓨팅 효율이 안좋을 것 같아 보이지만, 그에 대해서는 후술한다.

Central Frequency Offset 제거

Central Frequency Offset은 Tx와 Rx가 중앙 주파수를 서로 못 맞춰서 벌어지는 일이다. 이때까지의 오류 원인들은 모두 서브캐리어마다 다르게 작용하여 Normalize한 CSI 값에도 영향을 주었으나, Central Frequency Offset은 모든 서브캐리어에 동일하게 더해지기에 Normalize 결과에 영향을 주지 않는다. 따라서 하나의 밴드를 레퍼런스 삼아 다른 밴드를 캘리브레이션한다면 CFO는 고려하지 않아도 되게 될 것이다.

어떻게 캘리브레이션하냐면... [업데이트 예정]

Unused Subcarriers 메꾸기

CSI에서 보고되는 서브캐리어에는 일부가 빠져 있다. Atheros CSI Tool의 경우 아래의 $Ng=1$, Intel CSI Tool의 경우 20MHz 대역폭에서는 $Ng=2$, 40MHz 대역폭에서는 $Ng=4$를 보고한다.

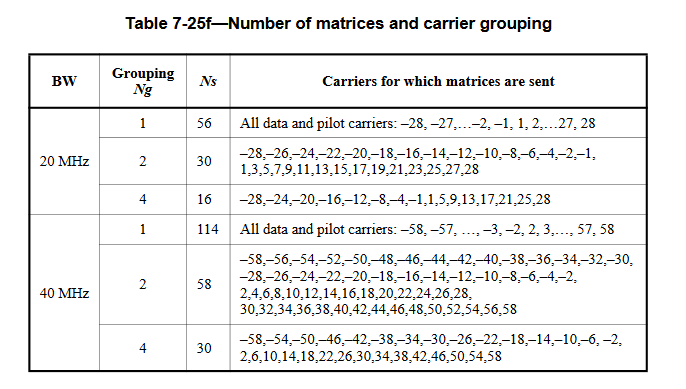
어떤 툴을 써도 중앙의 DC(Central) 서브캐리어와 양쪽의 가드 밴드는 보고하지 않는다. 각각 DC Offset과 인접 채널의 영향을 막기 위해서이다. 이러면 사실상 측정하려는 밴드에 대해 연속적으로 샘플링을 하지 않는것이 되는데, 통신 이론에 따르면 특정 대역폭($B_c$) 안의 주파수 대역은 페이딩을 비슷하게 겪는다고 하며, 실내 환경에서 $B_c$는 10MHz를 넘는다고 한다. 즉, 보고되지 않은 아이들은 커브 피팅으로 보완해줄 수 있는 것이다.

어떤 커브를 썼느냐면... [업데이트 예정]

Phase 값 이어 붙이기 마무리

아직 더 오류가 남아있을 수 있지만 (Thermal Noise, AGC Error 등) 이렇게 각 신호/패킷 분석 과정에서 일어나는 오류는 보상하고 여러 밴드의 Phase값을 이어붙일 수 있다.

이어붙인 다음에 한 번 더 SFO 보상을 해줄 수 있는데, 이어붙인 넓은 Bandwidth에서 일부 서브캐리어를 연속으로 선택하여 윈도우로 만들고, 그 윈도우들끼리 SFO 보상 알고리즘을 다시 한 번 실행하여 더욱 정확하게 SFO 값을 없앨 수 있다고 한다.

윈도우의 크기가 클 수록 더 정확한 SFO를 얻을 수 있을 것으로 보이지만, 그게 아니다.

따라서 전체 Bandwidth의 0.75를 사용하여 SFO 보상을 하면 가장 정확하며, 이렇게 이어붙이고 보상을 해줄 수 있다.

Amplitude 값 이어 붙이기

AGC에서 발생하는 Power Control 오류 또한 가우시안 분포를 따른다고 한다. 허나 이는 밴드와 무관한 현상이므로, Phase에서 평균을 내는 방식과는 다르게 얻은 모든 CSI값을 평균내어 구할 수 있다.

어떻게 했냐면... [업데이트 예정]

오류 보상 주기

올바른 이어붙이기를 위해서는 언제 CSI를 측정하여 시시각각 달라지는 오류를 보상해줄지 그 스케쥴링 또한 필요하다. 하지만 지금 내 목표는 이미 기록된, Windowed CSI에 대한 후처리이기 때문에, 여기 부분은 읽지 않았다.

T. S. Rappaport, et al., Wireless Communications: Principles and Practice. Upper Saddle River, NJ, USA: Prentice Hall, 1996. [본문으로]
A. Goldsmith, Wireless Communications. Cambridge, U.K.: Cambridge Univ. Press, 2005. [본문으로]
M. Speth, S. Fechtel, G. Fock, and H. Meyr, “Optimum receiver design for wireless broad-band systems using OFDM. I,” IEEE Trans. Commun., vol. 47, no. 11, pp. 1668–1677, Nov. 1999. [본문으로]
아래 말할 Central Frequency Offset으로 인한 오류는 여기에 영향을 주지 않는다! 왜 그런가에 대해서는 후술한다. [본문으로]

저작자표시 비영리 변경금지