2020년 08월 26일 05:08무선 네트워크/Channel State Information

Frequency Offset Estimation and Correction

본문

in the IEEE 802.11a WLAN

원문 : E. Sourour, H. El-Ghoroury and D. McNeill, "Frequency offset estimation and correction in the IEEE 802.11a WLAN," IEEE 60th Vehicular Technology Conference, 2004. VTC2004-Fall. 2004, Los Angeles, CA, 2004, pp. 4923-4927 Vol. 7, doi: 10.1109/VETECF.2004.1405033.

이 글은 단순히 읽은 논문을 정리한 것이다.

이 논문에서는 뭘 하는가?

파일럿 신호인 STF와 LTF를 이용한 Coarse & Fine Frequency Offset Tracking을 진행한다. 검증은 AWGN까지 구현된 완전한 802.11a WLAN 시뮬레이터로 진행한다.

IEEE 802.11a PHY 레이어

아래 내용을 읽으면서 OFDM을 다시 떠올리는 데는 Keysight의 Concepts of Orthogonal Frequency Division Multiplexing (OFDM) and 802.11 WLAN 문서와 WLANpedia의 OFDM in WLAN 문서를 참고했다.

$8\mu s$의 STF와 LTF, $4 \mu s$의 OFDM Symbol이 있다.

Short Training Sequence

총 10번의 동일한 파트($t_0 ~ t_9$, 각 $0.8\mu s$)로 나뉘며, 각 파트마다 16번 샘플링하도록 구성되어 있다.
시간 동기화, AGC 설정, 안테나 선택, Coarse FO Estimation에 쓰인다.
(가정) 위 쓰임 중 나머지는 모두 성공했고, 마지막 Coarse FO Estimation에는 $t_5 - t_9$만을 사용한다고 하자.

Long Training Sequence

하나의 Guard Interval과 두 개의 동일한 Training 파트($T_0, T_1$)로 나뉘며, 각 파트마다 64번 샘플링하도록 되어 있다.
Guard Interval은 $1.6 \mu s$, 두 Training Field는 $3.2\mu s$이다.
Guard Interval은 $T_1$의 마지막 32 샘플을 이용한 Cyclic Prefix이다.
Channel 추정과 Fine FO Estimation에 쓰인다.

OFDM Symbols

$0.8\mu s$의 Guard Interval과 $3.2\mu s$의 Data Symbol로 구성되어 있다.
첫 OFDM Symbol은 SIGNAL 필드, 이후는 DATA 필드이다.

시뮬레이션 모델

시뮬레이터로 모든 검증을 진행했다고 하는데, 어떻게 환경과 오류를 모델링했는가?

채널 모델

논문 오류로 채널 모델이 정확히 표기되어 있지 않으나, 여기서 중요한 것은 채널 모델이 아니라 FO 부분이므로 대충 아래와 같이 정리하고 넘어간다.

레일리 실내 모델이고, 한 프레임을 받는 동안 채널 상태는 일정하다고 가정하자.
전파 지연($D_{rms}$)은 $20 - 200 ns$ 이며 최대 다중 경로 수($L$)는 Sampling Period($T_s$)에 대해 $1+ \left\lfloor {10D_{rms}/T_s} \right\rfloor$ 이다.

Frequency Offset 모델

한 Rx에서 FO는 하나의 Oscillator에 의해 결정되므로, Carrier Frequency와 Baseband에서 FO는 같다고 가정한다.

Carrier Frequency Offset (CFO) 모델

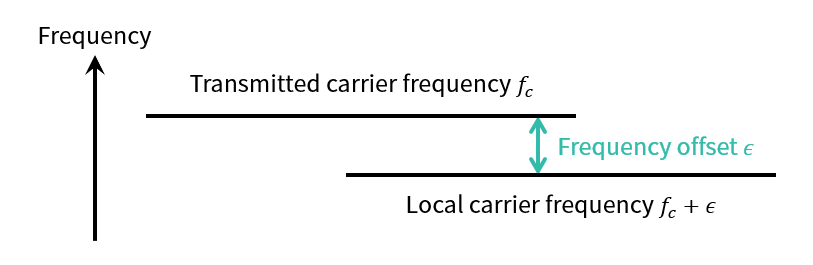
어긋난 Carrier Frequency에 의한 CFO Phase Shift Degree $\alpha$는 아래와 같이 나타낼 수 있다.

$$\alpha=2\pi\epsilon f_c T_s$$

$\epsilon$이 양수이면 샘플 당 Phase Shift $\alpha$ 역시 양수(반시계 방향)일 것이다.

이는 한 프레임의 $n$번째 샘플 신호에 대해 $e^{jn\alpha}$를 곱하면 CFO를 모델링할 수 있다.

Sampling Frequency Offset (SFO) 모델

어긋난 Sampling duration은 아래와 같이 나타낼 수 있다.

$$T_s'=(1-\epsilon)T_s$$

$\epsilon$이 양수이면 샘플링 기간은 짧아지고, 기존 샘플링 시각보다 이른 $\tau_n=n\epsilon T_s$에 샘플링이 이루어지게 된다.

이는 아래 그림과 같이 표현할 수 있다.

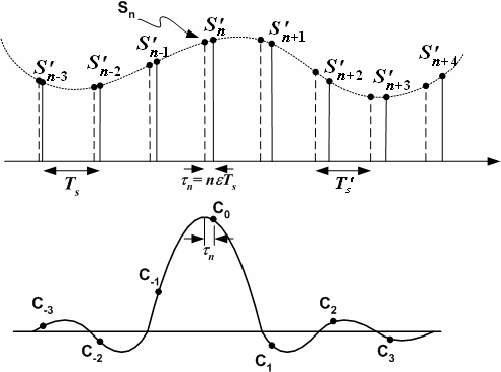
Calculating Offset Samples From The Ideal Samples

위쪽 그래프에서 실선으로 표시된 $S'$가 이상적인 샘플링 간격이며, 점선으료 표시된 $S$는 어긋난 샘플링 간격이다.

이 샘플링 오류 SFO를 모델링하기 위해서 이 논문에서는 Sinc LPF에 딜레이를 주었으며, 식으로 표현하면 아래와 같다.

$$C_m = Sinc(\pi(t+\tau_n)/T_s)|_{t=mT_s}=Sinc(\pi(m+n\epsilon)),\quad -\infty<m<\infty$$

이는 위 그림의 아래쪽 그래프에도 그려져 있다.

결국, CFO와 SFO를 모두 고려한 샘플은 $S_n=\sum^\infty_{m=-\infty}{C_mS'_{n+m}}$ 으로 나타낼 수 있다.

이 논문에서는 시뮬레이션을 돌리므로, $m$을 $-50<m<50$으로 유한히 한정한다.

Frequency Offset 추정 및 교정

아까 STF를 가지고 Coarse FO Estimation, LTF로 Fine FO Estimation을 한다고 했다.

위에서 $\alpha$를 실제 CFO로 거론했는데, 이 CFO 추정치 $\hat{\alpha}$를 구하고 그를 통해 CFO와 SFO를 교정할 것이다.

STF, LTF를 이용한 CFO 추정 및 교정

Step 1. STF를 이용한 Coarse CFO Estimation

아까 10개의 STF 중 $t_5-t_9$ 를 이용한다고 했다. 이들은 총 80개의 샘플로 이루어졌으며, 각 샘플을 $S_m$이라고 하자 ($m=0,1,\cdots,79$).

그러면 $\hat{\alpha}=\frac{1}{16}\angle \left(\sum^{63}_{m=0}S_m^*S_{m+16}\right)$ 으로 $\hat{\alpha}$를 나타낼 수 있다. 여기서 $\angle$은 $\pm \pi$ 사이의 Phase 값을 말한다.

이렇게 이 단계에서 대략 유추한 $\hat{\alpha}$ 를 $\hat{\alpha}_{ST}$ 라 하고, 다음 Fine Estimation으로 넘어가자.

Step 2. LTF를 이용한 Fine CFO Estimation

여기서는 두 개의 LTF를 모두 이용하며, 각 샘플을 $S_m;(m=0,1,\cdots,127)$ 이라고 하면 아래의 세 단계를 거쳐서 처리할 수 있다.

Coarse Correction. 각 샘플을 위의 $\hat{\alpha}{ST}$를 이용하여 보상한다. → $S_m=S_me^{-jm\hat{\alpha}_{ST}}$
Fine Estimation. 위와 동일한 방법으로, 하지만 조금 더 많은 샘플을 가지고 더 정확하게 FO Estimation을 수행한다. → $\hat{\alpha}_{LT}=\frac{1}{64}\angle\left(\sum^{63}_{m=0}S_m^*S_{m+64}\right)$
Fine Correction. 1번과 동일한 방법으로 각 샘플을 보상한다. → $S_m=S_me^{-jm\hat{\alpha}_{LT}}$

STF, LTF 이후부터는 $\hat{\alpha}=\hat{\alpha}_{ST}+\hat{\alpha}_{LT}$를 이용하여 CFO를 교정할 수 있다.

또한 위에서 언급한 $\alpha=2\pi\epsilon f_cT_s$ 관계를 이용하여 첫 번째 FO 값 $\hat\epsilon_0$을 구할 수도 있다.

Pilot Subcarrier를 이용한 FO 추정 및 교정

STF와 LTF를 이용하여 CFO를 교정하고 나서도 부정확성에 의해 Residual CFO가 나타나고, SFO도 아직 남아있다. 이로 인해 FFT 결과값에서 위상 오차가 나타나는데, 이는 Pilot Subcarrier로부터 얻은 정보를 통해 교정해볼 수 있다.

이 논문에 따르면 OFDM 심볼과 서브캐리어에 따른 (이 단계에 진입했을 때) 남아 있는 위상 차이 $\phi_{l,k}$는 아래와 같다.

$$\phi_{l,k}=2\pi l\left(\epsilon_rT_uf_c-\frac{N+N_g}{N}\epsilon k\right)$$

여기서 $l$은 OFDM 심볼 인덱스, $k$는 서브캐리어 번호 (-26 ~ 26), $N$은 FFT Size (64), $N_g$는 GI의 샘플 수 (16), $T_u$는 OFDM Symbol 길이 ($4 \mu s$), $\epsilon_r$은 $\epsilon - \hat{\epsilon}_0$, 즉 Fine CFO Correction 이후 남아있는 CFO이다.

위 식을 살펴보면 $\epsilon_rT_uf_c$ 부분은 서브캐리어 인덱스와 관계 없이 공통적으로 적용되는 Residual CFO이고, $\frac{N+N_g}{N}\epsilon k$ 부분은 SFO임을 알 수 있다.

이 논문에서는 이 두 FO를 교정하기 위해 총 세 단계를 도입했다. 이 세 단계에서 사용하는 기호 표기는 아래와 같다.

[$\mathbf{H}$] 서브캐리어 $k$의 채널 이득을 $H_k$라 하자. $k$가 -26부터 26까지 존재하므로, $H_{-26},\cdots,H_{26}$이 존재할 것이다.
[$\mathbf{Q}$] 802.11a 기준으로 Pilot Subcarrier는 -21, -7, 7, 21이므로 이를 $Q$를 이용하여 $Q_{-2}=H_{-21}$, $Q_{-1}=H_{-7}$, $Q_{1}=H_{7}$, $Q_{2}=H_{21}$ 과 같이 나타낼 수 있다.
[$\mathbf{X}$] 수신 측에서는 받은 신호에서 [GI Dropping > 64-FFT] 를 수행하고, 그 중 48개의 Payload와 4개의 Pilot Symbol을 건져 낼 것이다. 각 Subcarrier의 Symbol을 $X_k$라 하자. 여기서부터는 Frequency Domain이다.
[$\mathbf{P}$] Pilot Symbol은 Pseudo-random 값을 제거하고 채널 추정 및 시간 동기화에 쓸 수 있는데, 이를 $P$로 나타내면 $P_{l,-2}=X_{l,-21}$, $P_{l,-1}=X_{l,-7}$, $P_{l,1}=X_{l,7}$, $P_{l,2}=X_{l,21}$ 이 된다.

Step 1. SFO 교정

직전 Symbol에서 계산한 Sampling Frequency Offset 추정 값 $\hat{\epsilon}_{l-1}$과 위에서 나온 식 $\text{SFO}=2\pi l \frac{N+N_g}{N}\epsilon k$ 을 사용해서 간단히 보상해줄 수 있다. 자세한 내용은 위에서 언급한 논문을 보면 나온다.

$\hat\epsilon_{0}$은 $\hat{\alpha}=\hat{\alpha}_{ST}+\hat{\alpha}_{LT}$ 와 $\alpha=2\pi\epsilon f_c T_s$ 을 이용해서 구한 $\hat\epsilon_0$ 이다.

$$X_{l,k}=X_{l,k}\exp\left(2\pi l \frac{N+N_g}{N}\hat{\epsilon}_{l-1}k\right),\quad k=-26,\cdots,26$$

$X$에 대해서 해주는 것이므로, 당연히 Pilot Symbol $P$에 대해서도 교정을 해 주는 것이다.

Step 2. Pilot Subcarrier를 이용한 Residual CFO 교정

위에서 말한 Residual CFO 부분($2\pi\epsilon_rT_uf_c$)은 모든 서브캐리어에 대해 공통으로 적용되며 OFDM Symbol 인덱스에 따라 일정하게 증가한다. 이는 $P$와 $Q$를 활용하여 나타낼 수 있다.

$$\hat{\beta}_l=\angle\left({\sum_{i=-2,-1,1,2}P_{l,i}Q_i^*}\right)$$

이를 이용하여 다시 한 번 보상해주면 아래와 같다.

$$X_{l,k}=X_{l,k}e^{-\hat{\beta}_l},\quad k\neq -21,-7,7,21$$

여기서 Pilot Symbol을 고려하지 않는 이유는 그 다음번 $\hat\epsilon_l$을 구해야 하기 때문이다. SFO Correction만 적용한 Pilot Symbol을 FO 추정에 사용하는 것과 관련해서는 위에서 언급한 논문을 보면 나온다.

Step 3. Pilot Subcarrier를 이용한 정밀한 FO 추정

이제 다음 OFDM Symbol의 SFO 교정(위 Step 1)에 쓸 $\hat{\epsilon}_{l}$ 값을 추정해야 한다.

이 논문의 저자는 관찰을 바탕으로 실제 Frequency Offset $\epsilon$이 LTF 기반 교정 이후 구했던 초기 추정값 $\hat\epsilon_0$과 Residual CFO $\epsilon_r$의 합이라는 것을 알아냈다.

한 OFDM Symbol 이후 Residual CFO로 인해 증가하는 위상 회전 값 $2\pi \epsilon_r T_u f_c$은 아래와 같이 현/전 심볼의 Pilot Symbol을 이용해 추정할 수 있다.

$$\angle(W_l)=\angle\left(\sum_{i=-2,-1,1,2}P_{l,i}P_{l-1,i}^*\right)$$

Training Sequence 뒤 처음으로 오는 SIGNAL OFDM 심볼의 인덱스가 1임을 기억하자. 해당 심볼에서 위 값을 구할 때는 $P_{0,i}=Q_i$로 놓을 수 있다. 즉, $\angle(W_1)=\angle\left(\sum_{i=-2,-1,1,2}P_{1,i}Q_{,i}^*\right)$이 된다.

연속적인 덧셈 연산은 Fixed-point 하드웨어에서 부정확한 계산의 원인이 될 수 있으므로 4개의 연속된 $W$를 Exponential 필터를 적용하여 아래와 같이 더해준다.

Addition : $V_l=\sum^l_{m=l-3}W_m$
Filter : $U_l=\rho V_l + (1-\rho)U_{l-4}$

$l=4k$ 단위로 연산을 수행하므로 결국 $U_{4k}=\rho(W_{4k-3} + W_{4k-2} + W_{4k-1} + W_{4k}) + (1-\rho)U_{4(k-1)}$ 이 된다. 아주 부드럽게 변화하는 값이 나올 것 같다.

이 논문에서 저자들은 파라미터 $\rho$ 를 경험적으로 $1/32$로 얻은 것 같다. 이제 이를 바탕으로 $\hat{\epsilon}_l$을 추정할 수 있다. $l=4$ 이전에는 $l=0$의 값($\hat\epsilon_0$)를 사용하는 듯하다.

$\hat\epsilon_r=\angle(U_l)/(2\pi T_uf_c),\quad l=4,8,12,16,\cdots$
$\hat\epsilon_{l}=\hat\epsilon_{l+1}=\hat\epsilon_{l+2}=\hat\epsilon_{l+3}=\hat\epsilon_{0}+\hat\epsilon_{r},\quad l=4,8,12,16,\cdots$

위에서 다룬 각 과정의 결과는 OpenOFDM의 이 문서에서 Constellation Map으로 볼 수 있다.

안테나 다양성을 활용한 FO 추정 향상

안테나가 여러 개 있어도 하나의 Oscillator로 작동하므로 CFO, SFO 보상에 활용할 수 있는 데이터의 수가 늘어나 더욱 정교하게 CFO, SFO를 교정해줄 수 있다는 내용이다. 주요 관심 대상이 아니라 자세히는 읽지 않았다.

시뮬레이션 결과

Left: RMS error after ST and LT processing, Right: RMS error after Pilot Symbol processing

왼쪽은 STF와 LTF를 이용한 Coarse/Fine CFO Correction 이후인데, 점선이 Coarse Correction, 실선이 Fine Correction 이후이다. 오른쪽은 Pilot Subcarrier를 이용한 교정 이후이다. 가면 갈수록 RMS가 더 낮아지는 좋은 결과를 얻었다고 한다.

다시 한 번 정리

CFO, SFO 교정 방법

STF에서 대충 CFO를 유추하여 $\hat{\alpha}_{ST}$ 라 하고, 그를 이용하여 교정한다.
남은 CFO를 LTF로 좀 정밀하게 유추하여 $\hat{\alpha}_{LT}$ 라 하고, 그를 이용하여 교정한다.
이 단계에서 SFO와 또 남은 자잘한 CFO가 존재하게 된다.
SFO와 Residual CFO를 Pilot Symbol과 Channel Gain을 이용하여 추정하고, 교정한다.

QnA

$\alpha=2\pi \epsilon f_c T_s$인 이유는 무엇인가?
Frequency Offset이 $\epsilon$이고, 각주파수(초당 라디안)의 식이 $w=2\pi f$이므로, 매번 샘플링을 할 때마다 $T_sw=2\pi\epsilon f_c T_s$만큼이 느려지게 된다. 따라서 매번 샘플링을 할 때마다 위상 회전은 $\alpha=2\pi \epsilon f_c T_s$ 만큼 발생한다.
왜 $\hat{\alpha}_{ST}=\frac{1}{16}\angle \left(\sum^{63}_{m=0}S_m^*S_{m+16}\right)$ 인가?
여기서 논문의 오류로 보이는 것이 있는데, $\hat{\alpha}_{ST}$는 사실 $\frac{1}{16\times 64}\angle \left(\sum^{63}_{m=0}S_m^*S_{m+16}\right)$가 되어야 한다고 본다. $\hat{\alpha}_{ST}$는 한 번 샘플링을 할 때마다 생기는 Frequency Offset의 정도인데, 위의 계산식은 16 hop의 샘플 차이가 나는 것을 총 64번 더했으므로 한 hop 차이가 나는 샘플 간의 Frequency Offset은 $16\times 64$로 나눠야 그 대략적인 평균값을 알 수 있을 것이기 때문이다. 이는 $\hat{\alpha}_{LT}$와 $\angle(W_l)$도 마찬가지로, $\hat{\alpha}_{LT}=\frac{1}{64\times 64}\angle\left(\sum^{63}_{m=0}S_m^*S_{m+64}\right)$ 와 $\angle(W_l)=\frac{1}{4}\angle\left(\sum_{i=-2,-1,1,2}P_{l,i}P_{l-1,i}^*\right)$ 가 되어야 한다고 본다. 이는 내가 논문 이해를 잘못한 것일 수 있으므로, 확신하지는 않는다.
LTF를 이용한 CFO Correction의 첫 번째 단계에서 왜 STF + Guard Interval만큼의 Phase Rotation은 보상해주지 않는가?

위 그림에서 볼 수 있듯이, $\hat{\alpha}_{ST}$와 $\hat{\alpha}_{LT}$를 활용한 CFO 제거 과정에서 두 LTF의 시작 부분에서부터 Sample 인덱스를 시작하기 때문에 그 이전의 STF와 GI 시간에 증가해 온 Frequency 차이는 보상이 이루어지지 않는다. 하지만 이 값은 상수 값에 가깝기 때문에 (기울기가 위에서 설명한 FO 보상으로 제거됨), Waveform을 보면 단순한 평행 이동으로 나타나게 된다. 이는 따로 "Timing Offset"이라는 용어가 있으며, 별개의 보상 방법을 따른다. 이는 이 내가 보려는 "Frequency Offset" 주제를 벗어나기에 굳이 이 글에서 따로 다루지는 않는다.
Residual CFO 보상을 할 때와 Pilot Symbol을 활용한 Fine FO Estimation을 할 때, $P_{0,i}=Q_i$와 같이 Pilot Symbol($P$)이 들어가야 할 것 같은 자리에 채널 이득($Q$)을 대입하는데, 이렇게 해서 위상 회전 값을 구할 수 있는 이유는 무엇인가?
모르겠다. 논문에서는 아무런 설명도 나와있지 않다.
위에서 나온 아래 말의 의미는 무엇인가?

연속적인 덧셈 연산은 Fixed-point 하드웨어에서 부정확한 계산의 원인이 될 수 있으므로 4개의 연속된 $W$를 Exponential 필터를 적용하여 아래와 같이 더해준다.
모르겠다. 논문에서도 저 말 이외에 설명 혹은 인용 없이 그렇다고 하는데, 잘 모르겠다.

저작자표시 비영리